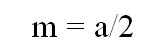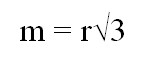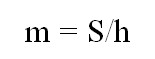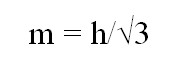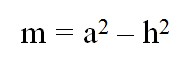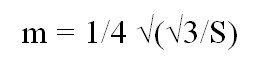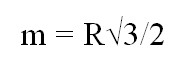Треугольник. Средняя линия.

Треугольник – геометрическая фигура. Состоит из:

• трех отрезков, не параллельных друг другу;
• трех точек, не лежащих на одной прямой.

Отрезки, являющиеся сторонами, соединяют точки - вершины треугольника между собой.

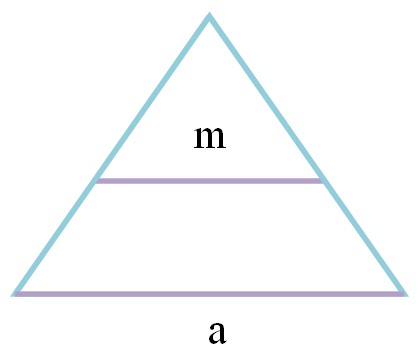
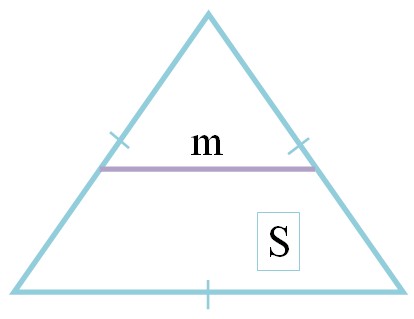
Если через середины двух сторон провести отрезок, то он будет средней линией треугольника. Отрезок, пересекающий середину одной стороны, проходящий через вторую сторону и параллельный третьей – главный признак средней линии.

Средняя линия:

• параллельна одной из сторон и равна половине ее длины.
• Делит треугольник на трапецию и, идентичный исходному, треугольник, уменьшенный в два раза. Площадь треугольника в 4 раза превосходит площадь отсеченного треугольника.

Проведя три средних линии одновременно, получается четыре треугольника. Их стороны, углы и площади идентичны. Фигура, получившаяся в середине, называется дополнительной или серединной. Если исходный треугольник равносторонний, то полученные путем проведения средних линий треугольники, также будут равносторонними.

По заданной длине средних линий легко вычислить периметр исходной фигуры. Нужно длины всех средних линий сложить, удвоив полученную сумму.

В любом треугольнике можно провести не больше трех средних линий.

Вычислить среднюю линию треугольника

Через сторону

Срединный отрезок равняется половине противолежащей стороны. Следовательно, формула выглядит так:

где a — противолежащая сторона.

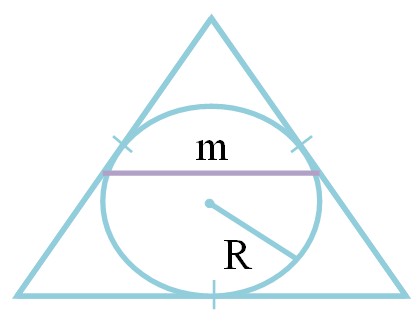
Средняя линия равностороннего треугольника через радиус вписанной окружности

Срединный отрезок равностороннего многоугольника через радиус вписанной окружности высчитывается так:

где r — радиус вписанной окружности.

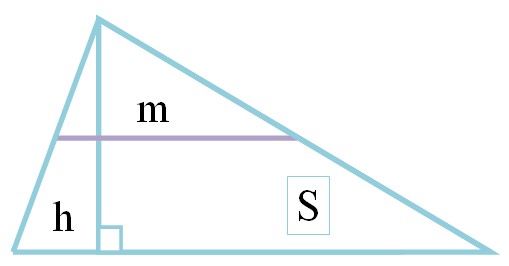
Средняя линия треугольника через площадь и высоту

Срединный отрезок многоугольника равен частному площади и высоты, перпендикулярной этой средней линии. Таким образом, тождество имеет такой вид:

Где S — это площадь, а h — перпендикуляр, ортогональный срединному отрезку.

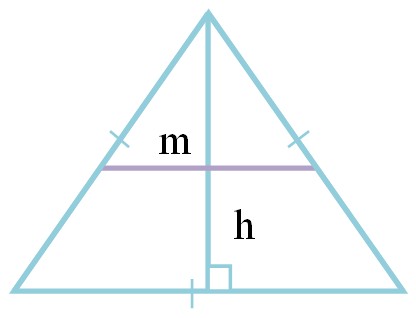
Средняя линия равностороннего треугольника через высоту

Срединный отрезок равностороннего многоугольника через перпендикуляр высчитывается следующим образом:

где h — перпендикуляр равностороннего многоугольника.

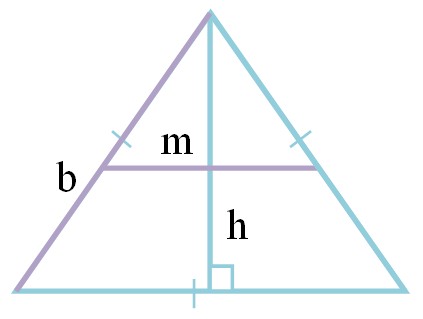
Средняя линия равнобедренного треугольника через боковую сторону и высоту

Срединный отрезок равнобедренного многоугольника через боковую сторону и высоту вычисляется следующим образом:

где a — боковая сторона, а h — перпендикуляр.

Средняя линия равностороннего треугольника через площадь

где S — это площадь равностороннего многоугольника.

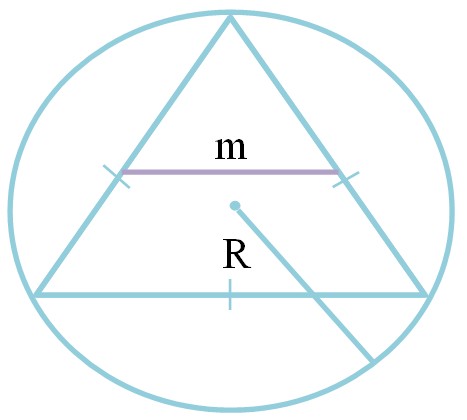
Средняя линия равностороннего треугольника через радиус описанной окружности

Срединный отрезок равностороннего многоугольника через радиус описанной окружности высчитывается так:

где R — радиус описанной окружности.