Геометрическая прогрессия
Геометрическая прогрессия - это название набора чисел a1, a2, a3…, в котором, при заданном первом числе a1, следующие числа получаются путем последовательного умножения предыдущего числа на одно и то же число (знаменатель прогрессии) q.
При этом справедливы условия, что ни первый член a1, ни знаменатель прогрессии q не могут быть равны 0.
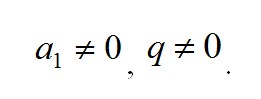
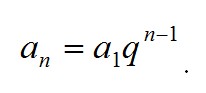

При положительном первом члене и показателе, большем 1 (), прогрессия возрастающая, при меньшем единице положительном показателе прогрессия убывающая. Если же знаменатель прогрессии отрицательный (), в прогрессии соседние члены чередуются знаками.
Замечательным (характеристическим) свойством геометрической прогрессии является то, что модуль значения каждого члена прогрессии представляет собой среднее геометрическое значение значений его соседних членов (предыдущего и последующего), откуда и название прогрессии (геометрическая):
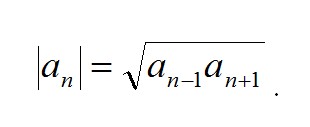
Сумма первых n членов геометрической прогрессии вычисляется по формуле:
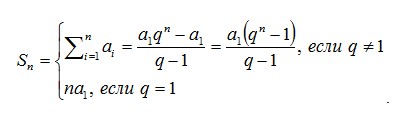
Произведение первых n членов геометрической прогрессии вычисляется по формуле:
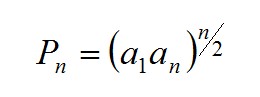
Примеры геометрической прогрессии:
1. 5, 15, 45, 135…
2. 1, -1, 1, -1, 1…
«Каждый из 7 египтян имеет по 7 кошек; каждая кошка ловит 7 мышей, каждая мышь съедает 7 колосков, из каждого колоска может вырасти 7 мер зерна.»
Легко убедиться, что здесь геометрическая прогрессия с первым членом 7 и показателем прогрессии также 7.
4. По геометрической прогрессии распространяются слухи. Если приезжий привозит в город новость, и сообщает ее в течение 10 минут 3 случайным жителям, а те, в свою очередь, распространяют ее таким же образом дальше, число жителей, знающих новость, можно подсчитать по сумме членов геометрической прогрессии:
1, 3, 9, 27, 81…,
т.е. слухи распространяются очень быстро.
